
今回のロジカルシンキング・トレーニングの題材は「演繹法と帰納法」
人間って色々な事を毎日考えて決断していますが、実はその思考方法には2つしかないんです。知っていましたか?
色々な事を考えて決断しているのに、その思考方法が2つしかないなんて驚きですよね。逆に言えば、そのたった2つの思考方法の使い方を知っておく事で、より論理的に物事を考えられるようになり、ありとあらゆるビジネスパーソンの強力な武器となります。
例えば2つの思考法を使いこなす事で、上司を説得しやすかったり、わかりやすい資料を作れたり。ちなみに、コンサルタントは「課題解決」が売りで、論理的思考力が物を言うので、この2つの考え方は徹底的に叩き込まれます。
そんな2つの思考方法は、演繹法と帰納法と言います。これは聞いたことありますよね。この2つの思考方法が、人間の思考方法の全てのベースになっているわけです。今回はこの演繹法と帰納法について、例題を用いて説明していきます。是非この機会に身につけてみてください。
ちなみに、この記事だけで演繹法と帰納法の基礎をマスターできるように、かなり情報量を詰め込んでいるため、相当な文字数になっています(約8,600字)。そのため、疲れたら適宜休憩しながら例題を解いて読み進めてみてください。読み終わった頃には演繹法と帰納法について、日常で使えるレベルになっているはずです。
人間の思考には2つしかない
まず人間には2つの思考方法しかないと言うのはどう言う事なのか考えます。
- お腹が空いたからご飯を食べよう
- 僕はいつか死ぬ
- 今度の旅行はアメリカに行こう
- 筋トレは有益だ
これらの結論は、2つの思考方法から導かれています。そうです、それが演繹法と帰納法。
ちなみに、どの文章が演繹法から導かれて、どの方法が帰納法から導かれているかわかりますか?
上2つが演繹法、下2つが帰納法です。この記事が読み終わった頃には、これよりももっと複雑な文章も、演繹法から導かれたのか帰納法か導かれたのかわかるようになるはずです。
ただまずは、演繹法とは?と言う基礎的な部分から確認していきます。
演繹法とは
演繹法とは、簡単に言えば「”当たり前と思われているルール”に”ある出来事や考え”を当てはめて”結論”を導く方法」です。
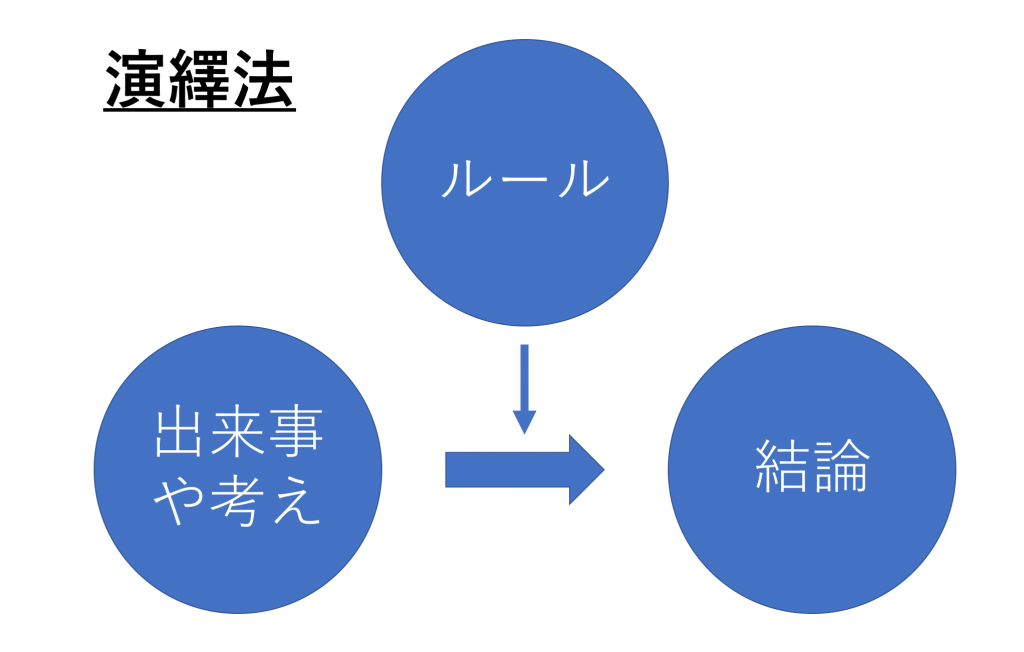
- 世の中で当たり前と思われているルール=大前提
- ある出来事や考え=小前提
- 結論=結論
と言うように、演繹法では大前提、小前提、結論と言う言葉を使います。で、これらを使った一連の思考の流れは以下の図です。
ある出来事が起こり、その出来事が世間一般のルールに当てはまる場合、結論が出ると言う考え。例を出した方が分かりやすいので、先ほどの「僕はいつか死ぬ」と言う結論を出すまでの思考過程を辿ると、以下の図のようになります。
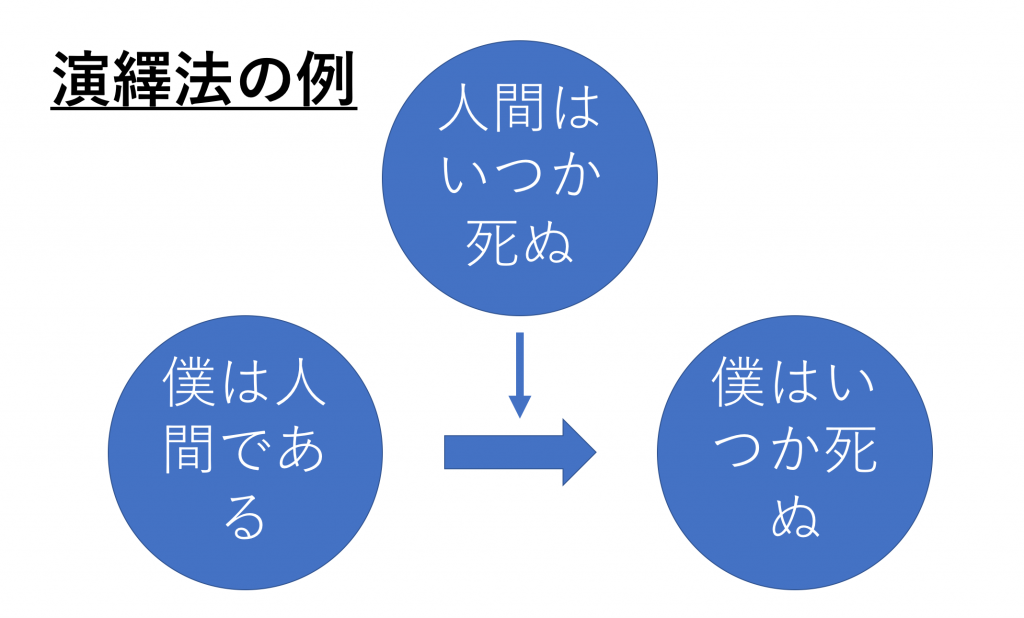
世間一般のルール、普遍的事実として「人間はいつか死ぬ」という大前提があり、「僕は人間である」と言う小前提、出来事(事実)がある。この「人間はいつか死ぬ」と言うルールに「僕は人間である」と言う事実を当てはめると、「僕はいつか死ぬ」と言う結論が得られるわけです。この、ある出来事をルールに当てはめて結論を出す思考を演繹法と言います。
では演繹法をより詳しく理解するために、例題を用いて説明します。
演繹法例題1
演繹法をマスターするための例題です。◯の中に入るルール(大前提)を考えてみて下さい。
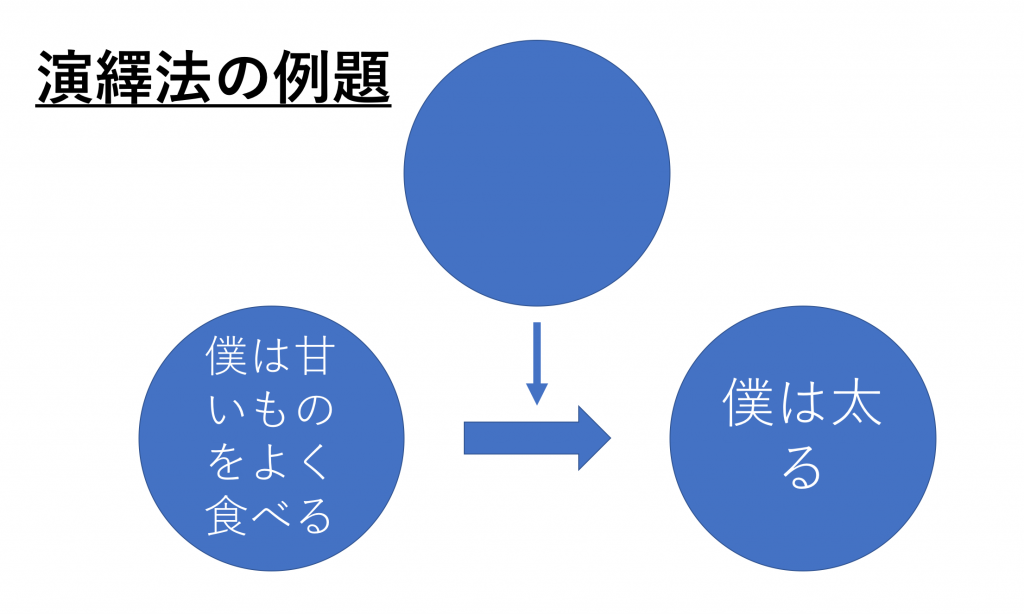
つまり、この場合はなぜ「僕は甘いものを食べると、僕は太るのか」、その理由がルールになります。
これは初歩の初歩のレベルの思考でなので、早速答えに行きます。
解答例とポイント1:ルールが正しいか確認する必要がある
ルールに入るのは「甘いものを食べると太る」になります。図にすると以下の通り。
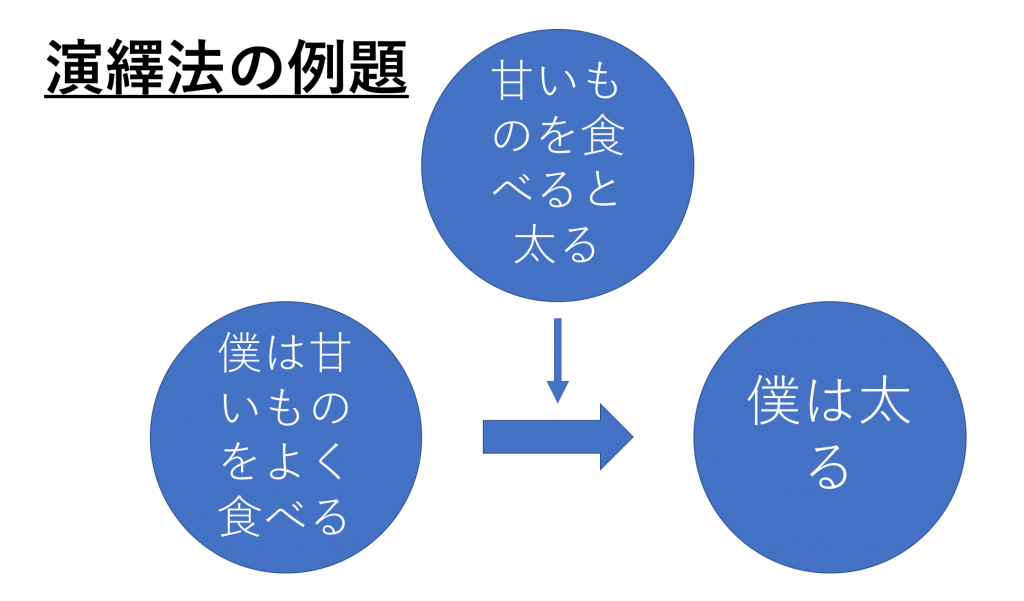
「甘いものを食べると言う一般的事実があり、「僕は甘いものをよく食べる」と言う事実がある。よって「僕は太る」と言う結論が導き出されるわけです。さて、どうでしょう。この理由にあなたは納得しますか?なんか納得できないと言う人もいるのではないでしょうか?
ここで演繹法で思考する時のポイント1つ目、「ルール(大前提)が間違っていると、自動的に結論も間違える」が出てきます。
今回の例のルールは「甘いものを食べたら太る」でした。しかしこのルール、おかしいですよね?なぜなら、甘いものを食べたからと言って太るとは限らないから。甘いものを食べる頻度や量次第ではもちろん太りますが、週一回に1つケーキを食べるくらいじゃ太りません。そもそも、甘いものってどれくらいが甘いものに含まれるのでしょうか?と、ルールが突っ込みどころ満載なわけです。ただ、あまり何も考えず「甘いものを食べたら太る」と聞いたら、「そうだよなー」と思ってしまうわけ。
これが演繹法のポイント1つ目です。つまり、演繹法を正しく使うにはまずルール(大前提)が正しいか確認する必要があります。正しいことが確認できて初めて、結論が正しい可能性が出てきます。
では、そもそもなぜ「甘いものを食べたら太る」と言うのをよく考えないでいると、「なるほど」と思ってしまうのか?そこを深掘りしつつ演繹法の2つ目のポイントをみて行きます。
演繹法例題2
先ほどのルール「甘いものを食べると太る」、これはそもそもどう言う思考過程で出てきたのか、下図の空欄を埋めてみてください。
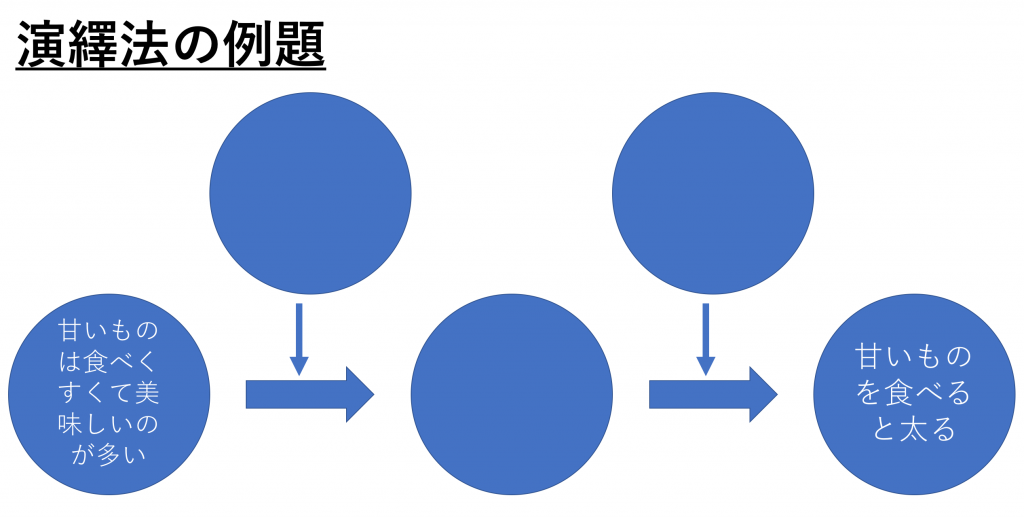
「甘いものは食べやすくて美味しいものが多い」と言う事象から、「甘いものを食べると太る」と言う結論に至るまで、今回は2ステップ踏んでいます。
今回も答えを見て考えた方が分かりやすいので、さっそく解答例を見て行きます。
解答例とポイント2:自分や相手の理解度に応じて論理を掘り下げる
「甘いものは食べやすくて美味しいものが多い」から「甘いものを食べると太る」と言う結論に至るまでの思考回路の一例は以下となります。
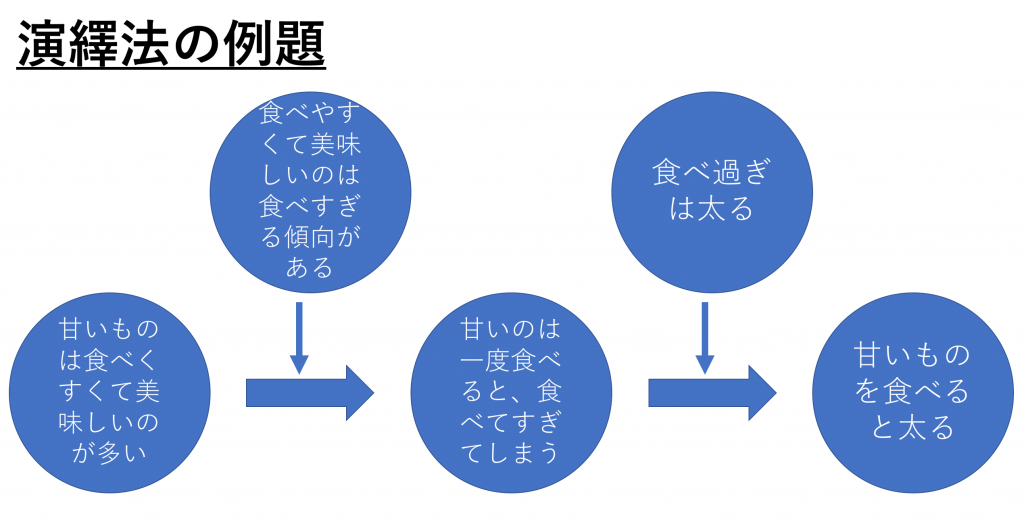
「甘いものは食べやすくて美味しいものが多い」と言う事象に対して、「食べやすくて美味しいものは食べすぎる傾向がある」と言うルールを当てはめて、「甘いものは一度食べると食べすぎてしまう」と言う結論を得ます。
そこから更に、この「甘いものは一度食べると食べすぎてしまう」と言う結論に対し、「食べ過ぎは太る」と言うルールを当てはめることで、「甘いものを食べると太る」と言う結論を得ることができました。
さて、この思考回路で示唆されるポイントは2つあります。
1つ目のポイントは、演繹法はまわりクドくなりやすいと言うこと。まず、この思考回路を見てあなたはどう思いましたか?
この思考回路がそもそも正しいのかと言うのは置いておくとして、やや回りくどいなと思いませんでしたか?
そうなんです。演繹法って、使いすぎるとクドいんです。だって、甘いものを食べると太るよねって言う話をする時、大抵の人は頭の中で自然と「甘いものはついつい食べすぎてしまって太る」と考えてるはず。それを一々上図のようにクドく説明する人はいませんよね。なので、大抵の人は日頃当たり前のように途中の思考を省略して考えている、話しているわけです。
ただ、ここで2つ目「演繹法は、どれくらい省略して良いかが難しい」と言うポイントが出てきます。先ほど見たように、演繹法ってまわりクドくなりやすいから、普段は途中の思考回路は省略して使います。ただ、どれくらい省略して良いのかと言うのが時と場合によって結構違うわけです。
例えば、頭いい人と話していると、たまに「え?なんでそう考えたの?」と思うことがあります。これは、頭のいい人が当たり前と思っていることと、僕が当たり前と思っていることが異なるためです。
もう少し分かりやすく詳しく説明すると、
「AIが普及しても、人間の仕事ってなくならないよね」
って言われて
「え?なんで?」
と考える人がいる。前者は頭の中で「AIが普及すると既存の職がいくつかなくなるが、新たにAIに従事する職が必要になる。」って言う思考があるのに対して、後者は「AIは人と同じような思考をするので、人間が今まで考えていた仕事を奪う」と考えている。
明らかに前者の方がAIに詳しい人ですが、詳しいが故に「AIに従事する新たな職が生まれる」と言う考えを当たり前と思い、省略して話すわけです。ただ、後者はそこまで詳しいAIの知識がないために「AIが普及しても、人間の仕事ってなくならないよね」と言う言葉だけを聞いても「なんで?」と理解できません。
このように、意思疎通を図る両者が、同じ程度の考えや前提で話していないと、食い違いが生じて今います。両者脳内を図にすると下図になります。
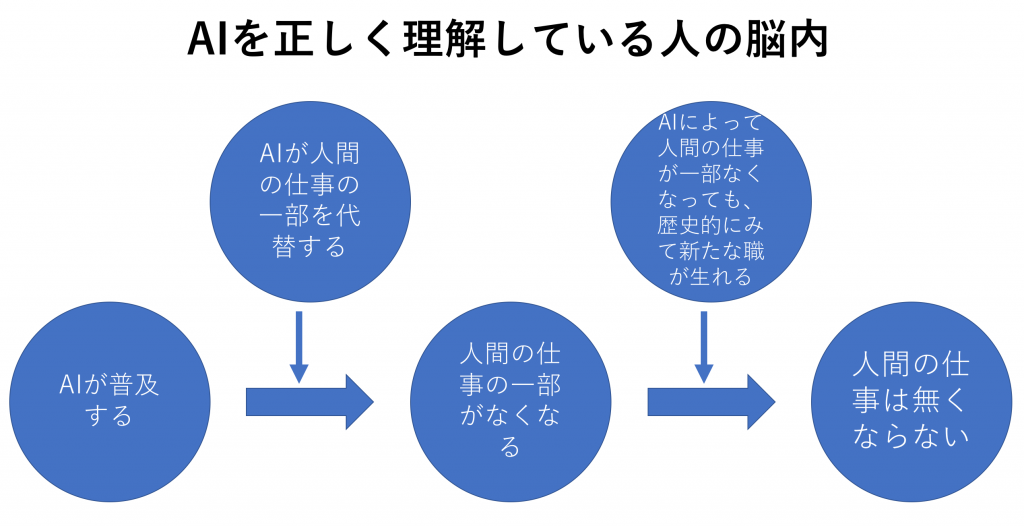
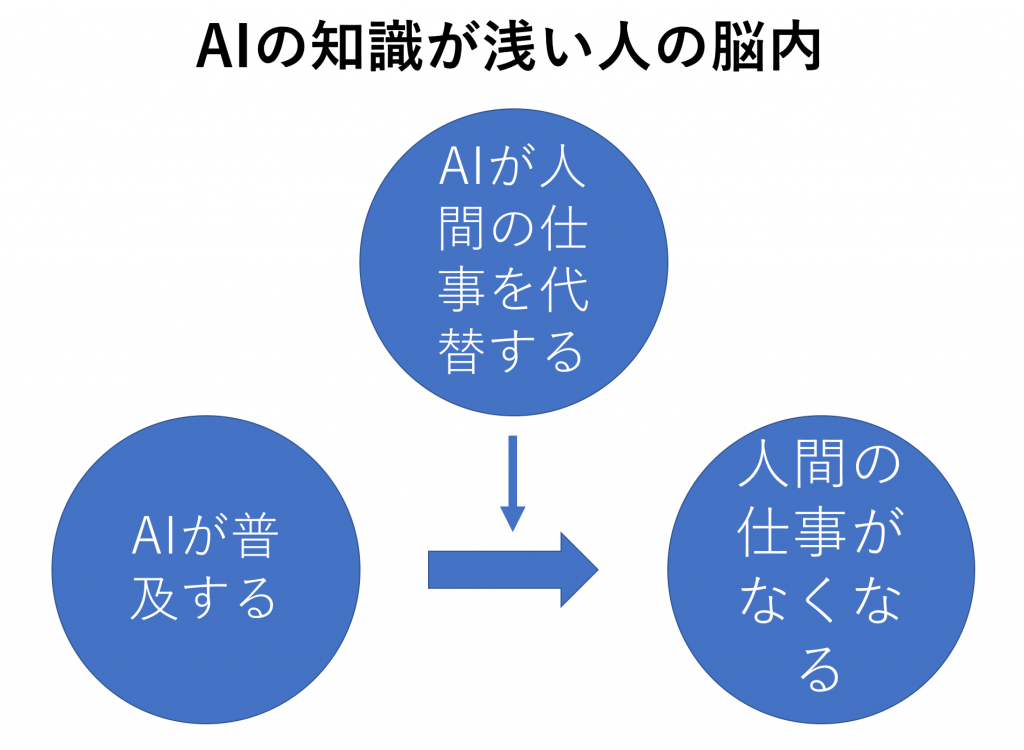
このように、両者の頭の中では異なる思考回路が形成されています。
AIや歴史についてよく勉強している人は、「AIが奪うのは人間の仕事の一部である」と言うことと、「歴史的にみて、新たな技術が台頭して人間の職を奪っても、また新たな職が生まれる」と言うことを理解しています。
後者について例として、産業革命時のイギリスで起きたラッダイト運動と言う、機械破壊運動が挙げられます。これは産業革命で機械が発達し、モノを作る仕事が機械に奪われるのではないかと不安になった人々が、機械をぶち壊していったと言う運動です。しかし結局政府の規制の下この運動は下火になりました。で、結局モノを作っていた人たちはどうなったかと言うことですが、徐々に新しい職に就きました。その中には機械を作る仕事に就く人も。つまり、新しい技術が台頭して一部の職が奪われても、その技術を支えるための新しい職が必要になると言うことです。
これを理解している人は、AIが台頭しても大丈夫と考えているので、「AIが普及しても、人間の仕事ってなくならないよね」となるわけですが、これを聞いた理解の浅い側は「なんで?」となってしまいます。
両者の理解度や置いている前提によって、どれくらい詳しく論理を掘り下げればいいか決めなくてはならないと言うのが、演繹法を使う上でやや難しいポイントとなります。
(AIについては、ラッダイト運動と異なり、本当に人間の仕事を奪うという考えもあり、有識者でも見解が分かれているところです。これについてはまた記事を書こうと思いますが、今回はあまり深く考えず、あくまで”理解度の異なる場合の例”としてみていただけたらと思います)
以上、演繹法を使う上でのポイントをまとめると
- ルール(大前提)が間違っていると、自動的に間違った結論に達してしまうので、演繹法を使う際にはまず、ルールが正しいか確認する必要がある
- 演繹法は一々説明するとクドくなる傾向があるが、かといって省略しすぎても相手に伝わらないことがある。そのため、相手の理解度に応じて詳しく論理を展開したり、省略したりする必要がある
この2点を、演繹法を使う際には気をつけてみてください。飛躍的に正しい論理展開ができるようになるはずです。
次は帰納法についてみていきます。
帰納法とは
帰納法とは、簡単に言えば「いくつかの出来事や考えから一つの結論を導く方法」です。図に表すと以下の通り。
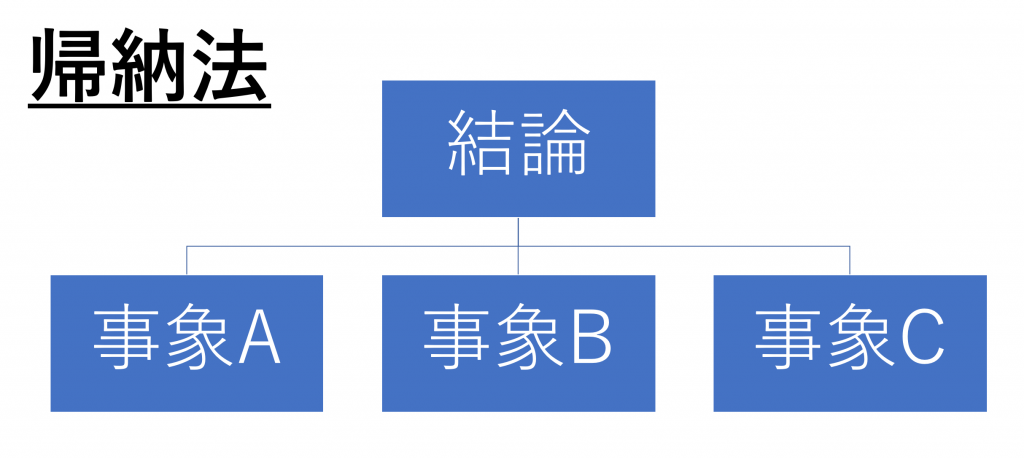
ある出来事や考えが3つA、B、Cとあり、その出来事や考えから1つの結論が導かれると言う構造になっています。これも例で考えた方がわかりやすいので、先ほどの「筋トレは有益だ」と言う結論を出すまでの思考回路を辿ると、以下の図のようになります。

「モテる」「健康になる」「頭が良くなる」、だから「筋トレは有益だ」と言う結論が導かれるわけです。
この例題の場合、「なぜモテる、健康になる、頭が良くなるからと言って筋トレは有益なの?」と疑問を持つ人は少ないかと思います。ただ、今回は誰もがそう思えるような例題にして、理由もそれなりにMECEを意識したから特に疑いなく納得できたのであって、事象(理由)によっては納得感のあまりない結論になってしまいます。
それについてはこの後の例題の解答例とポイントで説明します。
帰納法例題1
ではまずは帰納法を使用する際に最も重要な能力、「要約力」を試す例題です。3つの出来事を要約して、ツリー頂上の空欄を埋めてください。
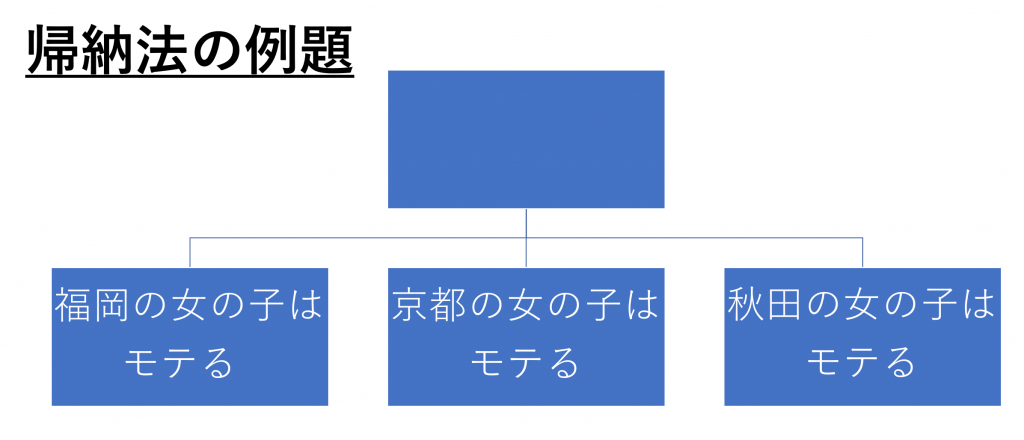
「福岡の女の子」「京都の女の子」「秋田の女の子」に共通するものを探し、それを要約したものを頂上に埋めればいいのです。さっそく解答例を見ていきます。
解答例とポイント1:帰納法とは要約である
例題の解答例は下図の通り。
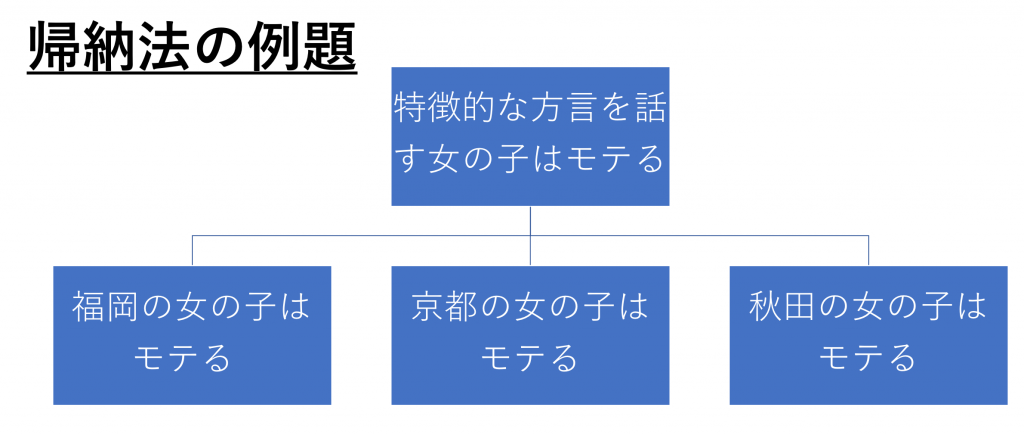
つまり、今回は僕の頭の中では、「福岡の女の子」「京都の女の子」「秋田の女の子」に共通するものは「特徴的な方言を話す」、と言う考えがあったので、3つをまとめて「特徴的な方言を話す」と要約して上位の概念に置きました。
さて、この解答例どうでしょうか?
もしかしたら人によって違う答えが導き出されたかもしれません。例えば「おしとやかな女の子はモテる」みたいな(福岡、京都、秋田の人がおしとやかなイメージがあればこう要約されてもおかしくない)。別にそれはそれで間違いというわけではありません。この3つのサンプルだけなら、「方言を話す〜」「おしとやかな〜」どちらでも違和感がないからです。
ここで一つ目の帰納法のポイント、「要約力が必要」が出てきます。要約力とは簡単に言えば、「物事の共通事項を見つけて、それを短い言葉で表す力」です。今回僕は「福岡、京都、秋田の女の子」を要約して「特徴的な方言を話す女の子」としました。しかしこれが、「日本人の女の子」と要約すると誰でも違和感を感じるでしょう。日本には47都道府県もあるのに、3県だけ見て「日本人の〜」とするのはやや論理が飛躍している感じがあるからです。
このように、いくつかの事象を正しく要約する能力が帰納法では必要になってきます。演繹法ではルールと事象さえ正しければ、自動的に正しい結論が導かれるのに対して、こちらは元となる事象が正しくても、必ずしも正しい結論が導かれるわけじゃないところに、帰納法の難しさがあります。
ではなるべく正しい要約、納得感のある要約にするにはどうすれば良いのか。ポイントは2つあります。
- 次元を揃える
- 必要十分なサンプル(事象)を用意する
です。この2つを気をつける事で、正しい要約がしやすくなります。では、こちらもどう言うことか、例題を用いて説明していきます。
帰納法例題2
まず、次元を揃えるとはどう言うことか。これについてはこちらの記事で詳しく説明しています。
簡単に説明するには図を見た方が早いので、上記事の図を抜粋しますが、詳しくは上記事を参考にして見てください。
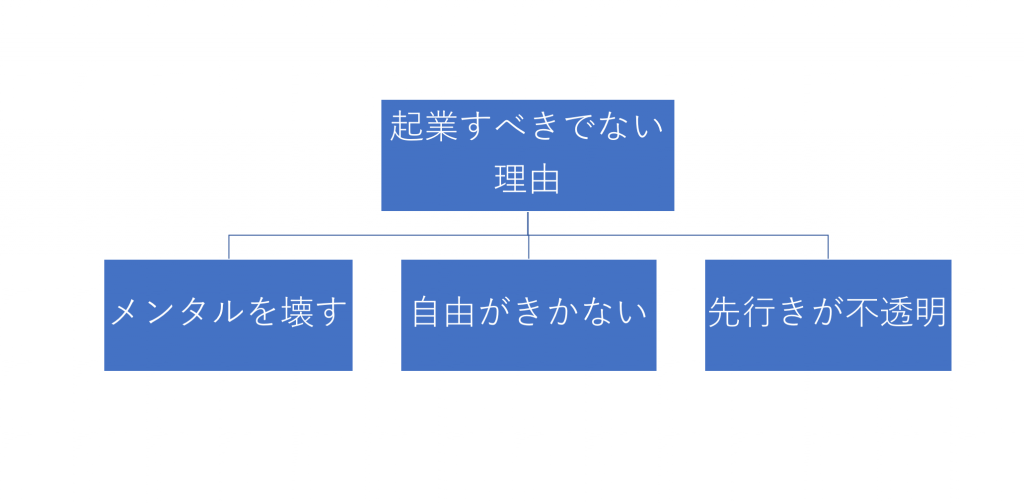
これは「起業すべきでない理由」を帰納法により導き出したものです。ただこの帰納法の使い方、ややおかしいところがあります。どこかわかりますか?
解答例とポイント2:次元を揃える
このロジックツリーを正しい帰納法に基づいて作成すると、以下の図のようになります。

実は、「起業すべきでない理由」が「メンタルを壊す」からであり、「メンタルを壊す」理由が「自由がきかない」「先行きが不透明」であるわけです。
なぜこの構造の方が良いかと言うと、ズバリ先ほど言った「次元を揃える」が満たされているから。この次元をいう言葉がやや難しい感じを醸し出し出していますが、一度わかっちゃえば簡単です。次元を一言で言えば”レベル感”の事。
例えば、「いちご、メロン、みかん」。この3つの括りはレベルが等しいです。同じ果物なので。でも、「東京、アメリカ、フランス」はおかしい。東京は都市なのに、アメリカ・フランスは国なので。これを”レベル感が違う”と言います。このレベル感を揃えないと、帰納法から正しい結論を得られなくなります。
ただこの次元、先ほどの「いちご…」「東京…」のような”事実”を考えるときはそれほど気にしなくても、簡単に同じレベル感で揃えられるのですが、”考えや行動”の場合はそうはいきません。考えとはまさしく「起業すべきでない理由」というようなもの。行動とは「生産性を向上させる」のような事。
なぜ”考えや行動”だと次元を揃えるのが難しいかというと、ズバリ”考えや行動には絶対的な次元が存在しないから”です。これについても上記事で詳しく書いてあるのですが、要は”考えや行動”は原因にも結果にもなり得るという事。
例えば、”生産性を向上させる”の場合。これは”大量生産するために生産性を向上させる”という文脈で使えば”生産性を向上させる”は下の次元に配置されますが、”生産性を向上させるために人員を確保する”という文脈で使えば上の次元に配置されます(下図参照)。
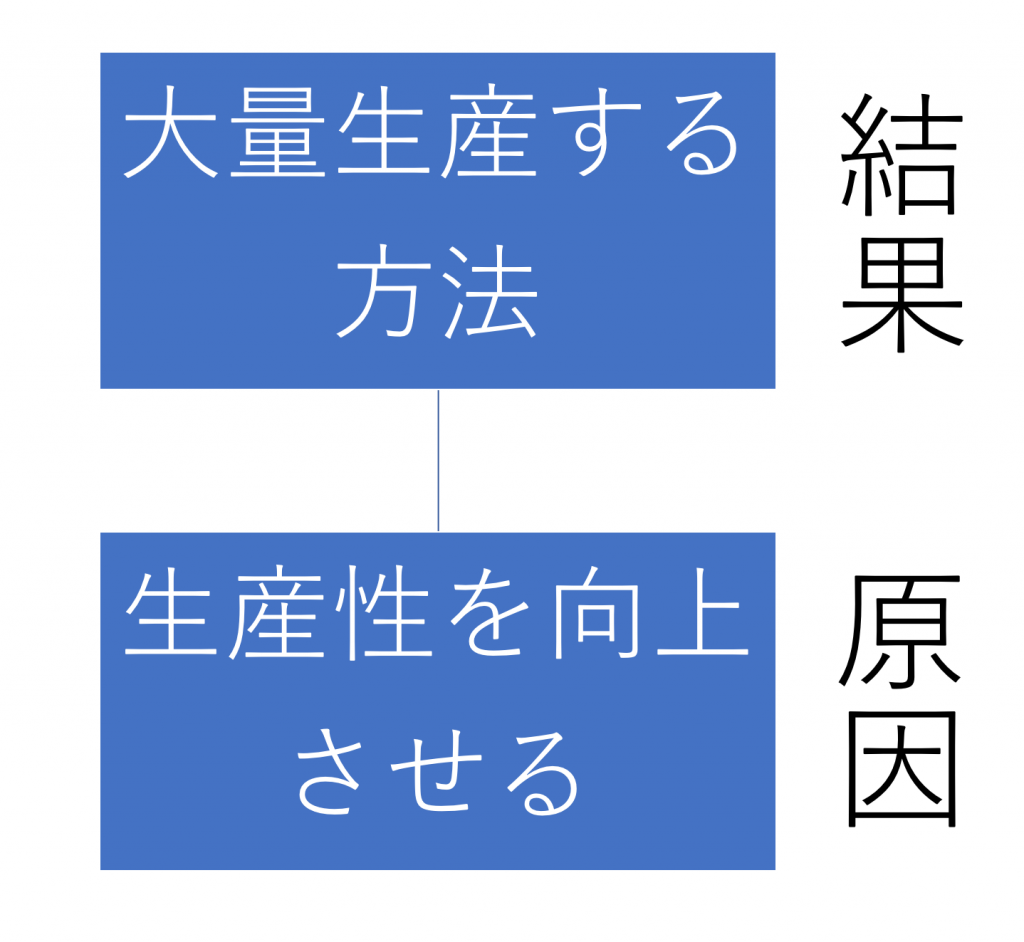

上図では、「大量生産するために生産性を向上させる」となり生産性を向上させるというのは、大量生産するための原因(方法)となっています。一方下図では、「生産性を向上させるために人員を確保する」となっていて、今度は生産性を向上させるというのは結果(目的)担っています。
このように、”考えや行動”は使われる状況によって上にも下にも配置されます。これを区別する方法は、上記事にあるように原因と結果を区別するしかありません。その練習は先ほどもリンクを貼りましたがこの記事で。もう一度リンクを貼っておきますので、この記事にある例題で、原因と結果を区別する思考を身につけてください。
帰納法例題3
納得感のある要約をするためのポイント2つ目、「必要十分なサンプル(事象)を用意する」を例題を用いて説明します。
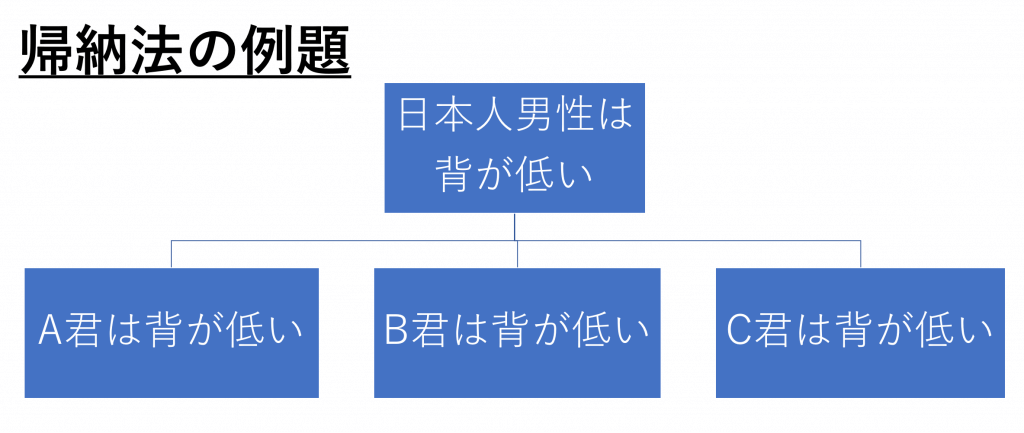
もしこのように「A君は背が低い」「B君は背が低い」「C君は背が低い」の3つの要約が「日本人男性は背が低い」だとおかしいですよね。なぜなら、この3つを見ただけで「日本人男性」と訳すのは無理があるから。
では、「日本人男性は背が低い」という結論を帰納法で導き出すにはどうすればよいでしょうか?
解答例とポイント3:必要十分なサンプル(事象)を用意する
このようにしたらどうでしょうか?
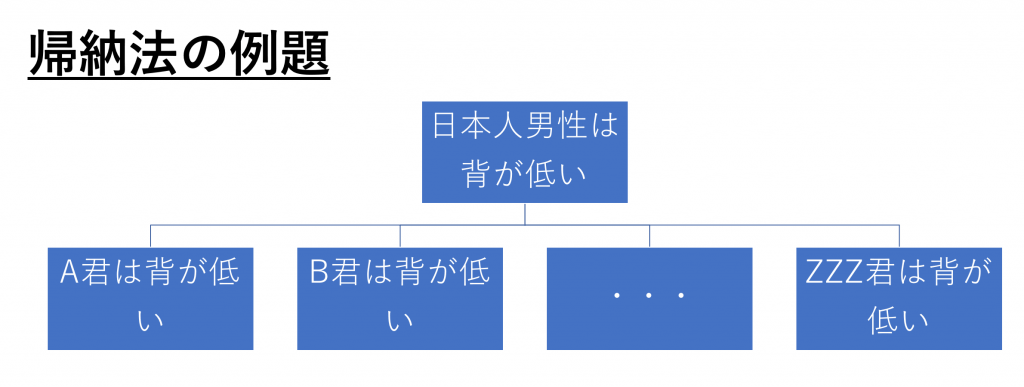
A君、B君、C君・・・AA君、BB君・・・AAA君、BBB君・・・ZZZ君の計17,576人
先ほどのA君、B君、C君だけの時よりは、納得感のあるツリーになったのではないでしょうか。このように、サンプルの数が増えれば増えるほど、帰納法はより正しく要約できるようになり、説明するときもより納得感のあるものとなります。
今回の場合は1万7千人のサンプルだけですが、これが10万人、100万人・・・と増えれば増えるほど、より正しい要約ができるようになります。逆に言えば、もっと多くの人を調べて見て、背が低くない人が多くいれば「日本人男性は背が低い」とは言えないことになります。
このサンプル数が多い方が正しい要約をしやすいという考え方は、”事実”だけでなく”考えや行動”にも当てはまります。例えば、先ほどの”起業すべきでない理由”。これも理由(サンプル)が多ければ多いほど、より強い理由づけとなり、納得感も増します。
もちろん、ただ不用意にサンプル数や理由づけが多くてもクドくなるだけです。必要に応じて量を要するのが良いでしょう。例えば、「本を読んだ方が良い」という考えを伝えるときに、本を読むメリットを3つくらい挙げれば大抵の人にとっては十分なわけです。これが10個も20個も説明されてもただクドくなるだけ。メリットのインパクトが大きい順に3つ選んで伝えましょう。
ポイントまとめ
今回は人間の思考方法はたった2つしかない事を説明し、その2つの思考方法「演繹法と帰納法」について、例題を用いて考え方を書きました。長くなったので改めてまとめておくと、
- 演繹法とは、ルールに出来事や考えを当てはめて結論を導く方法である
- 帰納法とは、いくつかの出来事や考えから一つの結論を導く方法である
そして、演繹法を使う際のポイントは、
- ルールが間違っていると、自動的に結論も間違えてしまうので、ルールが正しい確認する必要がある
- 演繹法はクドくなりやすいので基本的にある程度論理を省略するが、省略しすぎても相手に伝わらない場合があるため、自分や相手の理解度に応じて、柔軟に論理展開する必要がある
帰納法を使う際のポイントは、
- 帰納法を使うときは、いくつかの考えを要約する
- 正しく要約するために、事実や考え、出来事のレベル感を揃える
- 正しく要約するために、ある程度のサンプル数や理由づけを用意する必要があるが、多すぎてもクドくなるので、サンプルは多過ぎず少な過ぎずを心がける
以上全てのポイントをまとめておきました。
演繹法と帰納法は、ロジックツリーロジックツリーやクリティカルシンキングなど、ありとあらゆるロジカルシンキングのベースとなる考えです。それはなぜなら、人間は思考するときに必ずどちらかの方法で思考するから。
人間がどのように物事を考えているかわからないのに、思考のツールは使いこなせません。是非この記事の例題を参考にして、演繹法と帰納法を身につけてください。
そしてこの2つの思考法を身につけたら、ロジカルシンキングのツールで活かせるので、次はロジックツリーなどの技術を習得していきたいところです。

